For the next couple of posts, we’ll be talking about an important facet of computer security – hashing, hash codes, and especially what makes “cryptographically strong” hashes special. If you’re a developer or scripter and things stop making sense – let me know. It’s my fault, not yours.

One common problem in software is the desire to determine if two things (i.e.: files, documents, passwords) are the same or different without having to compare those things verbatim. For example, after downloading a huge file – how can you find out if it was corrupted during the transfer? It turns out that asking the web server, “Are you sure?” for every byte doesn’t really solve the problem.

One solution to this issue is called hashing: creating a small unique identifier for an item based on its properties or features. We use this concept all the time in real life: when describing people by their gender, height, race, and hair colour, or when quickly deciding if two files are the same by checking their name and size. This unique identifier is called a hash or hash code.

One thing the definition mentions is “based on its properties or features”. There are plenty of small unique identifiers that don’t qualify as hash codes: phone numbers, web addresses, and social security numbers, just to name a few. These are not derived from the thing they describe: you can’t look at somebody and decide that their social security number is 078-05-1120. Being able to independently create a hash code based on the inherent features of the item is crucial to its success. Along with being feature-based, the hash code for an item must be predictable. If two people calculate the hash code for the same item, they must arrive at the same answer.

Given these properties, we now have a good way to verify things like large file transfers. For example, many download links (such as the Visual Studio 2010 Trial) also document the hash code of the files:

(…) The CRC and SHA1 hash values of your generated ISO image should match these:

• CRC: 0x280d8d93
• SHA-1: 0x7790db7d2aac9e1ee8baa34d42988577689c9e7a

The terms CRC and SHA-1 are the names of two common ways to calculate the hash of a file. An other common way (aka: “Hash Algorithm”) is called MD5. In MD5, the hash code is often called the “MD5 sum.” After you’ve downloaded the file, you run a tool to calculate the hash code of the file and verify that it matches. A PowerShell script to do that is included in the PowerShell Cookbook (and on PoshCode.org): http://poshcode.org/2154.

More Pigeons than Pigeonholes!

One thing we had mentioned as a feature of good hash algorithms is that they return different hash codes for different items. But we also said that the hash codes must be shorter than comparing every bit of the item itself. A typical DVD download is about 5,000,000,000 bytes. A typical hash code is 256 bytes. This is a problem! Think about being asked to take the numbers 1 to 100 and represent them with a hash code that’s only one digit. Intuitively, you know it is impossible to identify 100 different numbers uniquely with only 10 numbers.

This is known in math and computer circles as the “pigeonhole principle” – if you have to fit 11 pigeons into 10 holes, at least one hole must have two or more pigeons. When you apply that to hash algorithms (representing a 5,000,000,000 byte file with 256 bytes), some of these files are going to have to share the same hash code. This is called a hash collision.

If you’ve only got 256 bytes to represent all possible files, minimizing these hash collisions is crucial. If our pretend 1-to-100 hash algorithm that uses only the digits 0-9 tends to cluster around the number ‘3’, you’re going to have more collisions than necessary. While this might seem obvious when you consider the entire range of possibilities, it should also apply to smaller portions of the range. If our hash algorithm for the numbers 1-100 just used the first digit, we’d have nothing but collisions if you only checked the numbers 10-19. Or only checked the numbers 20-29. To make a hash algorithm as effective as possible, designers try to make the algorithm distribute its answers as close to randomly as possible.

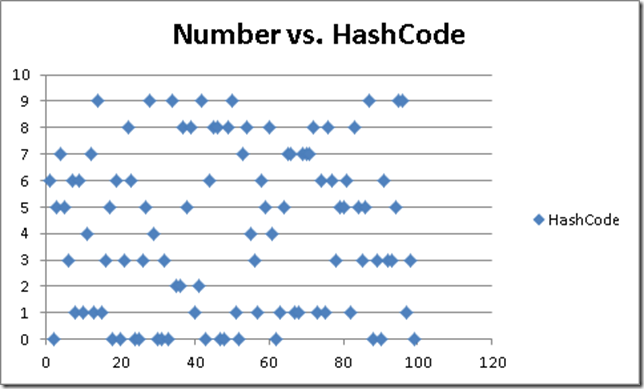
Not truly random, mind you. The hash code for an item must still be the same every time you figure it out: that is non-negotiable. Here’s an example of a bad hash code: ours.

Notice the clustering of collisions:

Take a look at a better one:

But Some People are Eeeevil

Using hash codes for simple content verification is one thing. But what if an attacker is trying to trick you with hash code collisions? For example, can you use that Visual Studio download if it’s from your worst enemy – but the hash code still matches? It depends on the algorithm! We’ll talk about the security implications of hash algorithms next.